僕が高校生の時、教育テレビで秋山仁さんの数学の番組を見た。
なんでか分かんないけどオカンが秋山さんの番組が好きで、見つけるたびに録画してくれてたんだよね。
はじめは「この人、すっげー稲川淳二とかぶるなー」くらいしか思わなかったんだけど、数学の説明が超分かりやすくてグイグイ引き込まれてちゃって。
25年くらい前のことなのにまだ鮮明に覚えてる話もあって。
その話とは、、、鳩の巣原理!なんじゃそりゃー!
鳩の巣原理とは
これが鳩の巣原理。数学嫌いな人は、これだけでもうこの記事閉じるよね。数学って本当は面白いのに、こういう風に小難しく書くから人気出ないんだよなー。
ちなみにこの鳩の巣原理、なんで鳩の巣って名前が付いたかというと、もとはこんな考え方だから。
だいぶ分かりやすくなったよね。
「1ヶ月に32人とデートしたよー!」
「少なくとも1日ダブっとるやないかーい!」
ってのも鳩の巣原理。
こう書くと、数学にも愛着が湧いてくるよね。わはは。
感激した問題
で、面白くてテレビに釘付けになって見てたら、最後に問題出されたんだよね。
問題文はものすごく単純で、状況も簡単に理解は出来るんだけど、「こんな問題どうやって解くんだよ!」って感じで全然分からなくって。でも、こんな問題もあるんだなーってなんか感激しちゃって。
その問題がこちら。
7m×7mの正方形の板に銃弾を50発撃ち込んだ時、50個の穴のうち2点間の距離が1.5mより短い組合せが少なくとも1つあることを示せ
え?全然感激しないって?
うんまあ、普通はあんまり感激しないと思うな(笑) この感激を理解してくれるのは、愛すべき高校の同胞たちくらいしか思いつかん。特に心の友Kスケくん。
さて僕はこの問題を見て解こうとしたものの、「50個から2つの点を取り出す組み合わせは50×49÷2=1225通りもあるのかあ」とか検討違いな計算をしだしちゃったりして。しかもそこから筆が進まず、あえなく撃沈。
気がついてしまえば中学3年生にも解けるけど、大学入試でも使えそうなこの問題、みんな解けたかな?
じゃあ解答にまいりましょう!
解答はこちら
7m×7mの板を1m×1mの49個の板に分ける。そこに50個の弾丸を撃つと・・・おお鳩の巣原理の出番やー!
少なくとも1つの正方形には2つの穴が開いてることになるよね!
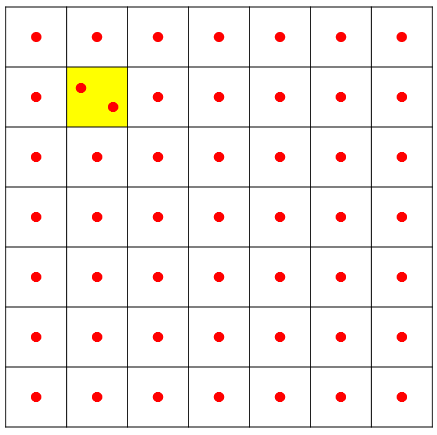
次にその2つ穴が開いてる正方形に着目した時、正方形の中で最も2点間の距離が開くのは対角線になる場合だよね。
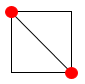
1辺1mの正方形の対角線の長さはルート2=1.414・・・<1.5m
よって題意は示された!いえーい!
まとめ
高校生の時に見たのに、ものすごく鮮明に覚えてるこの鳩の巣原理、なんとなんとあれから25年間1回も使うことなく40歳になってしまったわ(笑)
普通の生活を送るにあたって、ほんと一定レベル以上の数学って必要ないよなー。
今の中学生、高校生は何のために2次関数とか微分積分とか一生懸命やってんだろ?受験のため?ほんとこの国の教育制度は意味ないなー。その時間全部英語に充てたら、もっともっとグローバルな国になるのにね。
とはいえ、大人になってから趣味的にやる入試数学って、人生がかかってないから気楽に楽しめるし、頭の体操としてもほんと面白いなー。
あんなりいないと思うけど、数学好きな人、今度一緒にお茶しましょー!